原标题:基于机器学习的宏观因子模拟组合的构建
Introduction
1。作为《海外文学推荐丛书》的第59期报告,我们推荐伊曼纽尔·尤尔琴科(Emmanuel Jurczenko)和杰姆·泰利彻(rme Teiletche)在2019年发表的论文《Macro Factor Mimicking Portfolios》。
2。宏观因素在日常投资和研究中起着非常重要的作用。然而,由于宏观因素不能直接投资,如何利用宏观因素仍然面临巨大挑战。本文试图用因子模拟投资组合的方法来解决这个问题。
3。本文的主要贡献如下:首先,我们建立了因子模拟投资组合分析的一般框架。该框架可以包括各种常见因素模拟投资组合方法,如两步横截面回归和最大相关投资组合。其次,我们创新的机器学习方法在框架上改进了传统的因子模拟组合方法。最后,我们使用五种方法(四种传统方法和机器学习方法)构建模拟投资组合,并在模拟投资组合的基础上对冲典型投资组合的宏观风险。总的来说,本文提出的机器学习宏观因子模拟投资方法在杠杆率和拟合优度指数方面优于其他四种传统方法,在降低投资组合宏观风险和提高风险调整后收益方面具有显著效果。
4。宏观经济学对金融市场有着重要的影响,然而,我们不能直接投资于宏观因素。本文提出的宏观因素模拟组合有助于我们更好地解决这一问题,对于投资者将因素收益转化为可投资资产收益率具有重要意义。
风险提示:文献中的结果均由相应的作者通过历史数据统计、建模和计算完成。当政策和市场环境发生变化时,模型有失败的风险。“1、引言”要素投资的出现推动了投资者管理资产方式的一场重大革命。广义而言,要素是资产回报的基本驱动力(昂[,2014年),要素组合的回报来源于投资者暴露的一些系统性风险。要素投资的主要优势在于,它减少了投资者在构建投资组合时需要考虑的维度。如果选定的因素能够很好地预测资产回报率,那么投资者就可以专注于研究一组因素,而不是分别研究投资组合的每个组成部分。事实上,要素投资并不是一个新事物,在学术文献中已经有了广泛的研究(如资本资产定价模型(CAPM)和套利定价模型(APT models)。
然而,从理论到实践,投资者需要解决许多实际问题,例如,投资者需要根据经验选择潜在因素。我们知道许多学者对这个问题进行了相关的研究。例如,罗尔和罗斯·[1980];康纳和柯拉查克·[1988]使用主成分分析来构建潜在因素。法马和法属[(1992,1993)和卡哈特·[(1997)提出了一套基本要素分类方法,即价值、规模和动量。其中,宏观因素受到的关注较少。然而,陈等人([1986),昂和贝凯特[2004)认为宏观经济动态影响金融资产回报。宏观因素的主要问题之一是它们不能直接交易。解决这一问题的一种方法是将一些可投资资产类别与宏观经济指标联系起来,例如用股票衡量经济增长,用商品衡量通货膨胀(格林伯格等人,[,2016年)。
这个方法听起来非常简单实用。事实上,这种方法在选择重复宏观因素的资产类别时仍然是随机的,没有足够的统计理论支持。因此,提出了一种更通用的方法——因子模拟投资组合(FMP),解决了如何基于不能直接交易的因子构建投资组合的问题。
本文的主要贡献包括以下五点:
首先,本文建立了最小方差因子模拟投资组合构建的一般框架。该框架可以包括所有当前流行的因素模拟投资组合方法,例如法玛和麦克白·[(1973年)、雷曼和适度[(1988年)使用的两步横截面回归(企业社会责任,两次通过横截面区域)、胡伯尔曼等人[(1987年)使用的最大相关投资组合方法(MSP,最大相关投资组合)和拉蒙特·[(2001年)。值得注意的是,本文建立的框架具有良好的可扩展性,投资者可以增加投资组合约束(如禁止卖空、流动性限制等)。)ac
第三,我们使用一组基本资产来构建我们的宏观因素模拟投资组合。据我们所知,以前的论文大多使用单一资产类别(股票或公司债券)来构建因子模拟投资组合。同时,所选择的基础资产可以通过期货/掉期衍生品或交易所交易基金等工具进行投资,具有现实意义。
第四,我们比较了不同因素模拟组合方法复制三个全球宏观因素(经济增长、意外通胀、经济压力)的能力。从实证结果来看,我们提出的基于机器学习的FMP方法在样本内外都优于常用的FMP方法。
第五,本文构建了一个实证案例来说明如何利用宏观因素模拟投资组合的结果来对冲典型投资组合的宏观风险敞口。我们发现宏观套期保值可以显著提高投资者的投资风险。
本文的框架如下:
在第二章中,我们介绍了常用的因子模拟投资组合分析方法,并提出了一个因子模拟投资组合分析框架,该框架可以包括所有常用的因子模拟投资组合分析方法。
在第三章中,我们讨论了如何在基于机器学习方法的框架下改进传统的因子模拟投资方法,以解决测量误差和变量缺失的问题。
在第4章和第5章中,我们构建了一个实证案例来说明我们方法的实际效果。
第6章总结了整篇文章。
2、宏观因子模拟投资组合分析框架
factor仿真组合(FMP)已成为许多学术文件的主要主题(巴尔杜齐和机器人蒂·[,2008年))。一般来说,因子模拟投资组合由两部分组成:
1)基础资产:可投资资产;
2)复制因子:不能直接投资的潜在因子。

基于因子模型(2-1)和对法玛和麦克白·[1973年的研究,形成了第一种流行的FMP方法,即两步横截面回归法。该方法的主要步骤包括两个步骤:第一步是构建基础资产收益率与因子值之间的时间序列回归方程,估计资产负荷;第二步:通过资产收益率和估计贝塔系数的横截面回归,获得每个因素的风险溢价。横截面回归的最初目标是使用因子定价,但是Fama[1976]提出,在第二步回归中获得的系数相当于使用资产收益率来模拟在第一步回归中使用的因子。通过这种方法构建的模拟投资组合对其希望复制的因素的暴露为1。同时,在法玛-麦克白方法中,横截面回归的第二步由普通最小二乘回归(OLS)进行。为了处理公式(2-1)中可能存在的残差方差和自相关问题,一些学者建议使用不同的回归方法进行改进,例如加权最小二乘法(WLS;李岑伯格和拉马斯旺尼·[1979])或广义最小二乘法(GLS;雷曼兄弟和谦虚的[(1988))。
第二种FMP方法首先由胡伯尔曼等人[1987年]和布里登等人[1989年]提出。
这种方法的目标是最大化每个FMP和感兴趣因素之间的相关性,所以它也被称为最大化相关性投资组合(MCP)。主成分分析法基于单变量回归得到每个因素的资产负荷,并通过求解最小方差方程得到每个FMP。拉蒙特·[2001]提出了一种类似的方法——经济跟踪组合(ETP)。虽然ETP和MCP的具体方法不同,但我们可以推断出ETP的权重与MCP的权重成正比,比例系数是基于资产回报率的各个因素的多元回归系数。



我们的框架有以下三个优点:
首先,通过最小化方差获得FMP投资组合是一种相对常见的方法(胡伯尔曼等人(1987年)率先使用这种方法。Melas等人(2010年)、Roll和Srivastava (2018年)、Pukthuangthong等人(2019年)也提到了这种方法。然而,许多学者一直将这种方法与特定的FMP方法相结合,在本文中所有的方法都表示为一个通用公式。
其次,在公式(2-2)或下面的其他应用程序中,除了目标敞口之外,我们没有添加任何投资组合约束。然而,我们的框架允许投资者根据自己的需要添加各种形式的约束。例如,默认的FMP是一个长短组合,投资者可以根据实际情况限制他们可以做的数量。然而,它不应该
第三,尽管在上面的分析表达式中,我们只考虑静态β(例如,FMP权重)。然而,我们的框架也可以很容易地适应动态测试。例如,我们可以采用费森和哈维·[(Harvey,1991)提出的方法,通过使用滞后的宏观经济变量或特定资产工具变量来实现动态贝塔。
3、基于机器学习方法的因子模拟投资组合

不同于标准OLS估计。两步最小二乘四回归可以得到因子负荷的无偏估计。这主要是因为第一主成分能够在旋转不确定性的情况下恢复资产收益率的真实因素空间(白和吴[2002)。
直观地说,由于基本资产收益率与潜在风险因素完全不同,单个资产收益率中包含的信息可以用来恢复真实因素结构,并通过消除观测因素中的测量误差来提高FMP估计。
接下来,我们介绍一些机器学习方法来改进两步最小二乘FMP估计方法。在回归的第一步,我们用监督主成分分析代替了传统的无监督主成分分析方法,它在提取统计因子时明确地将基础资产的预测能力纳入到每个宏观因子中。在机器学习文献中,至少有三种方法可以提高回归预测能力。
第一种方法是使用偏最小二乘法提取统计因子(凯利和普鲁特·[,2015年)。
第二种方法是:缩放主成分分析(sPCA黄等人([,2018]),个人电脑是从一组基本资产回报中提取出来的,这些回报是根据它们各自对这些因素的预测能力进行缩放的。
第三种方法是:目标主成分分析(tPCABair等人([,2006),Bai和Ng[,2008]),使用硬或软阈值规则从对目标因素具有强预测能力的基础资产子集中提取个人电脑。
基于最后一种方法,我们使用软阈值LASSO惩罚规则来估计观测因子的拟合值。软阈值规则侧重于选择套索收缩参数,该参数可以通过最小化贝叶斯信息准则来选择。
最后,用机器学习方法得到的贝塔值代替传统OLS回归得到的贝塔值,我们就可以得到毫升-南车。
4、宏观因子模拟组合实证准备
对于任何宏观因素模拟投资组合方法,您都需要选择一组基本资产。在我们的实证研究中,基础资产不仅需要可投资,而且考虑到我们的实证研究始于20世纪70年代初,我们希望这些基础资产具有悠久的历史。
图表2列出了我们最终选择的九项基本资产。它们涵盖主要资产类别,如股票、政府债券、信贷、通胀债券、大宗商品和外汇。对于非指数价差的基本资产,收益计算为现金利率(1个月美元伦敦银行同业拆放利率)的超额收益。同时,大多数基础资产可以通过衍生品(期货或掉期)或交易所交易基金进行投资。
接下来,我们将使用这种方法来讨论因子计时中的几个重要问题,这有助于提高我们对因子计时的理解。

至于宏观因素,我们参考Ang(2014)并考虑三个全球宏观因素:经济增长、意外通胀和经济压力。
1)经济增长:由经合组织综合领导力指数(CLI)衡量,该指数可以捕捉全球商业周期的转折点。此外,该指数消除了长期趋势的影响,是衡量全球经济增长趋势的创新指标。
2)意外通货膨胀:可以用幼儿发展同比通货膨胀率指数的实现值与延迟6个月的值之间的差额来衡量。
3)经济压力:我们使用两个流行指标的等权重组合来衡量,即芝加哥联邦储备银行的国家金融形势指数(NFCI)和周[1999年开发的动荡指数]等。
为了便于解释,本文将ZSC的经济增长、意外通货膨胀和经济压力这三个因素标准化,并将波动性定为每月1%。数据样本期为1974年1月至2018年6月(534次观察)。近50年的数据窗口涵盖了各种宏观经济事件,如石油危机或20世纪70年代的几次经济衰退以及众所周知的市场崩溃。
为了构建宏观FMP,我们需要建立一个将基本资产收益与要模拟的宏观因素联系起来的因素模型。为了说明金融资产能够在经济事件发生前起到反应的作用,我们使用时间t-12的基本资产收益率与时间T的因子值回归,同时,为了消除滚动造成的重叠效应,我们使用纽维-韦斯特(Newey-West)估计调整后的T统计量来度量变量的显著性。图表3显示了OLS的回归结果。可以看出,这组基本资产对各种宏观因素的所有回归都具有统计显著性,其R在4%至33%之间。
Lehman and Membert[1988]指出,用于构建因子模拟投资组合的基本资产必须充分分散在因子负荷中,以便能够有效地复制因子。例如,较高的经济增长对股票、信贷和工业产生积极影响,同时对名义债券产生消极影响。意料之外的通货膨胀有利于与通货膨胀挂钩的债券、名义债券、黄金和能源,并将对美元产生负面影响。经济压力对股票、信贷、黄金、能源和美元收益产生了负面影响。

如第三章所述,宏观经济变量具有固有的噪声,这可能影响因素模拟投资组合的效果。因此,我们采用机器学习方法来改进传统的因子模拟投资方法。对于每个宏观因素,我们首先基于tPCA(前面提到的目标主成分分析)提取潜在因素。之后,通过LASSO回归选择相关的单个资产成分,并对tPCA拟合的宏观变量进行估计。最后,对于每一项基本资产,我们建立了其收益率与tPCA之间的回归方程。这里,我们用OLS后套索代替普通的OLS。该方法减少了变量维数,同时避免了套索回归中可能出现的低估问题。
图表4显示了机器学习因子模型的回归结果。可以看出,机器学习因子模型(调整R2)的解释力远远大于标准模型。我们还注意到,虽然LASSO模型用于个人电脑选择,但大多数个人电脑仍然保留,这表明考虑的宏观因素对于基本资产的回报率非常重要。

下面我们用不同的方法构造宏观因素模拟投资组合:
I)OLS:OLS-南车FAMA-麦克贝斯模型;
ii)GLS:FMP;基于协方差矩阵估计的GLS校正因子模型:
iii)WLS:FMP;基于协方差矩阵估计的WLS校正因子模型:
iv)MCP:unit-beta MCP
v)ml:ml-CSR,基于机器学习方法改进了第一种方法的OLS模型。
图表5显示了基于不同方法构建的模拟投资组合的结果。可以看出,一些基本资产在不同的FMP方法中显示出一致的风险敞口。例如,FMP的经济增长是着眼于许多股票、工业金属和通胀相关债券,以及国债。FMP对于意外通胀的看法是看低名义政府债券和美元,以及股票、通胀相关债券、信贷和黄金。面临经济压力的FMP将着眼于更多的政府债券、能源和美元,以及股票和信贷。其他资产的暴露在不同的方法中是不同的。

图表6显示了不同因素模拟投资组合的样本内表现。可以看出,FMP货币基金组织的杠杆(所有增加的头寸)远没有那么极端。这是一个关键优势,因为杠杆通常与风险相关,对一些投资者来说是有限的。相反,修正协方差组合通常会导致更高的杠杆作用。
我们发现M1 FMP获得的投资组合的波动性更合理,接近宏观因素的原始波动性(即当我们构建这些因素时为1%)。我们使用相关系数、RMSE、MAE等指标来衡量FMP与潜在因素的相关程度。从市场经济协会指数来看,蒙特利尔银行FMP分行表现最好,其次是蒙特利尔银行,而OLS南车银行表现最差。
图表6还给出了风险溢价(由每个FMP的超额收益率定义)和相关的夏普比率。可以看出,在所有因素上,只有OLS和FMP表现出积极的回报。同时,意想不到的通货膨胀因素具有最高的回报,所有方法都是正回报。然而,经济压力大多是负回报,这表明尽管经济压力会影响资产价格,但它们不一定有正溢价。

图表7显示了基于移动通信公司社会责任的FMP时间序列。本文使用
1)方法1(定长法):以1974年1月至1996年3月的数据为训练集,1994年4月以后的数据为测试集。
2)方法2(扩展样本法):从1996年4月开始,模型将每月根据扩展样本进行重新估计,新估计的FMP将用于下个月。
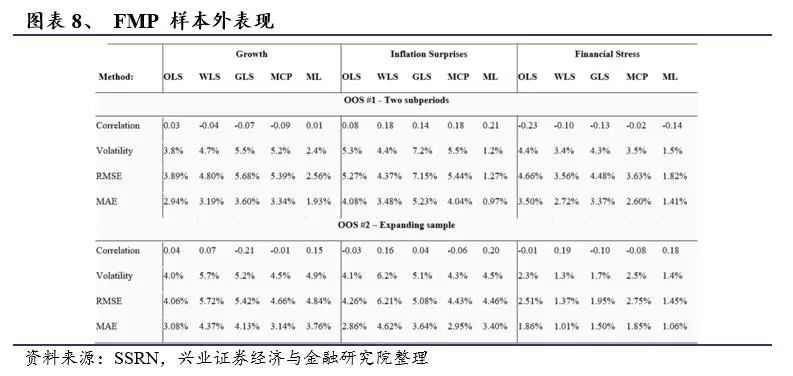
图表8显示了两种样本外方法的性能。可以看出,几乎所有样本外方法的拟合优度指标都有所下降,甚至一些因素的相关系数也发生了逆转。综合比较,FMP方法在样本外表现最佳。
5、实证案例:对冲典型基金组合的宏观风险
在前一篇文章中,我们从一个更一般的角度给出了不同因素定时能力下定时策略的表现,并给出了一系列盈亏平衡点。那么在实践中,我们能达到多高的因素计时能力,以及我们能否达到这些盈亏平衡点?在这里,我们从两个非常简单的时间策略开始观察因素时间策略在实践中的作用
宏观因素模拟投资组合的潜在优势之一是允许投资者对冲投资组合中包含的宏观风险,如经济衰退、意外通货膨胀和经济压力。
让我们以一个有代表性的投资组合为例。投资组合的构成如下:35%的股票(MSCI世界指数)、10%的政府债券(彭博巴克莱全球政府债券指数)和5%的高收益美国债券(彭博巴克莱高收益美国债券指数)。5%的商品(彭博商品总回报率指数)、20%的对冲基金、10%的房地产(NCREIF指数)和15%的私募股权(剑桥联合指数)。
首先,为了从宏观角度探索这个投资组合,我们基于扩展窗口方法建立了投资组合超额收益率与三个宏观因素之间的回归方程。具体的回归结果如图9所示。
我们分别基于去年12月的集成电路平均值和长短组合比率构建了要素动量策略和估值价差策略。两种策略的风格集成电路分别为19.13%和12.36%,基本达到了上述的盈亏平衡点,尤其是要素动量策略,超过了双方手续费数千美元的盈亏平衡点。这证明上述因素计时能力并非遥不可及。

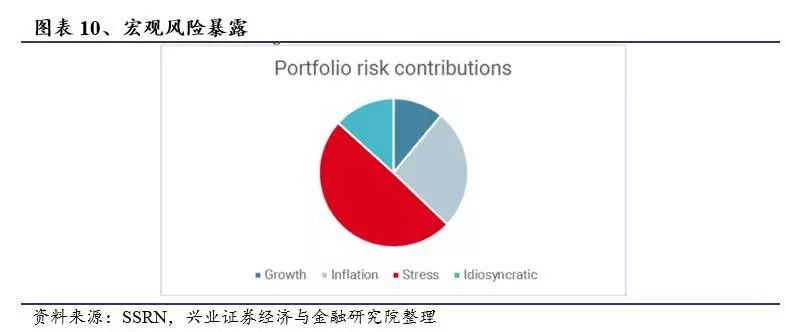
可以看出,模型的调整后R2接近90%,组合的年α平均值接近2.5%。接下来,我们计算投资组合风险贡献(使用波动率作为风险)。可以看出,投资组合中最大的风险来自经济压力,其次是经济增长和意外通胀。特殊风险约占投资组合总风险的10%。


图表12显示了这两种投资组合的表现。可以看出,尽管宏观对冲组合的年化回报率有所下降,但在波动性、最大回撤、夏普比率等指标上有了显著改善。同时,从总体分布来看,宏观套期保值后的组合表现也更好(偏斜为正,峰度降低)。

6、总结
宏观因素在日常投资和研究中发挥着非常重要的作用。然而,由于宏观因素不能直接投资,如何利用宏观因素仍然面临巨大挑战。资产定价文献中提出了许多处理非贸易宏观经济因素的方法。这些方法可以统称为“因子模拟投资组合(FMP)”。
本文提出了一个通用的FMP框架,它可以包括现有的因子模拟投资方法,如两步横截面回归法和最大相关投资组合法。
同时,我们在基于机器学习方法(如监督主成分分析和套索回归)的框架内改进了传统的FMP估计方法。基于五因素模拟投资组合方法(四种传统方法和机器学习方法),分别构建了三个宏观因素(经济增长、意外通货膨胀和经济压力)的模拟投资组合。可以看出,机器学习宏观因子模拟投资组合方法在杠杆率、拟合优度等指标上表现较好。同时,我们利用机器学习的宏观因素来模拟典型投资组合的宏观风险,可以看出,宏观套期保值后的投资组合在最大退出率和夏普比率上都有显著增加。
冰毒
参考文献
[2]昂 阿和格 贝卡尔特(2004),《中国日报》制度如何影响资产配置“,金融分析师杂志60,86-89
[3]白杰和吴士荣(2002),《中国日报》确定大维度因素模型的数量“,计量经济学70,191-221
[4]白杰和吴士荣(2008),《中国日报》使用目标预测器预测经济时间序列“,计量经济学杂志146,304-317
[5]白杰,特 哈斯蒂,德119-137
[6]巴尔杜齐 普和C罗博特蒂(2008),《中国日报》模拟投资组合、经济风险溢价和多贝塔模型的检验《》商业经济统计杂志26,354-368
[7]贝贝 阿、布兰特和路易西(2015),《中国日报》提炼宏观经济新闻流《》金融经济学杂志117,489-507
[8]贝罗尼 阿和维 切尔诺祖科夫(2013),《中国日报》模型后的最小二乘法“消费导向资本资产定价模型的实证检验”,《吗金融杂志《44,231-262
[10》卡哈特 姆(1997年)《中国日报》共同基金业绩的持续性“,金融杂志52,57-82
[11]陈北,北罗尔和S罗斯(1986),《中国日报》经济力量与股票市场“,商业杂志59,383-403
[12]周庚,杰奎尔,男克里茨曼和K劳里(1999年)《中国日报》最优投资组合“均衡中的风险和回报——新测试方法的应用”,《吗金融经济学杂志21,255-289
[14]康纳G和r科拉查克(1991年)《中国日报》美国共同基金的属性、行为和表现“,数量金融和会计评论1,5-26
[15]法玛E(1976),《中国日报》金融基础“,基础书籍,395页文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险
往
证券研究报告:《西学东渐--海外文献推荐系列之五十九》。
对外发布时间:2020年年年1月16日
-
证券研究报告:0103010。
对外发布时间:2020年年年1月16日
-
-
联系人以下内容以下内容:郑兆磊
电子邮件: zhengzhaolei
电子邮件: zhengzhaolei
-
电子邮件: zhengzhaolei